John Watson is a Menace to Society

---

I was recently sent a short clip from an anime by the name of “Moriarty the Patriot” by a friend and active follower of the blog (shoutout to Anais!) The clip, a grand total of two seconds in length, features an animated version of Dr. Watson from the Sherlock franchise throwing Sherlock Holmes a train ticket after a particularly heated debate. What may seem like a perfectly innocuous action, though, starts to fall apart when you analyze it closely. So grab your popcorn, relax, and let me show you– step by step– how John Watson can generate a force equivalent to the Hiroshima bomb with a flick of his wrist.

Let’s start at the very beginning. The portion I will be referring to throughout this post is 12:43 to 12:45 in Episode 10. We can already spot a few oddities in the first few milliseconds of the clip: the ticket appears to ignore drag– as if it were a credit card– while it’s flying towards Sherlock’s face, but it does descend slowly afterwards, as if affected by air resistance. This selective particle behavior pisses me off, so I’ll be taking this opportunity to set some ground rules:

1. We will be treating the ticket as if it was always subject to the same type of drag, meaning I’ll be letting the first blatant violation of the Laws of Physics slip.
2. We will be treating the ticket as a perfectly rectangular surface, as can be seen while it’s airborne, giving it a drag coefficient (C_d) of 1.28 as per NASA. The argument could be made that any sort of airborne paper would be folded, but the anime disagrees, so I disagree too.
3. We will be assuming the ticket is always subject to drag. This may sound obvious, but it will be important later on.

With that out of the way, we can finally get to the analysis part! The crux of this whole thing is the sound that the ticket makes when it hits Sherlock’s face is, for some reason, equivalent to that of a light slap (go see for yourself). Taking some figures from a Reddit post titled “If kinetic energy is converted into thermal energy, how hard do I have to slap a chicken to cook it?”, we can see that the average mass of a human hand is 0.4kg, and the average slap velocity is 11 m/s. With these two figures, we can calculate that the force exerted by a light slap is about (0.4kg)(11 m/s) = 4.4 Newtons.

Now this is all well and good for a slap, but what about the ticket? If the sound is equivalent, then the force must be roughly equivalent, too. That means the ticket is hitting Sherlock’s face with 4.4N of force as well, but remember that force depends partly on mass. That means we have to calculate the mass of the ticket to find its velocity as it hits Sherlock. To do that, we can compare it to the mass of a ream of paper (28.35g, or 0.02835kg) by finding how many tickets fit inside the ream’s size (8.5x11in, 22x28cm) and dividing the ream’s mass by that number. Let’s go ahead and find the ticket’s dimensions.

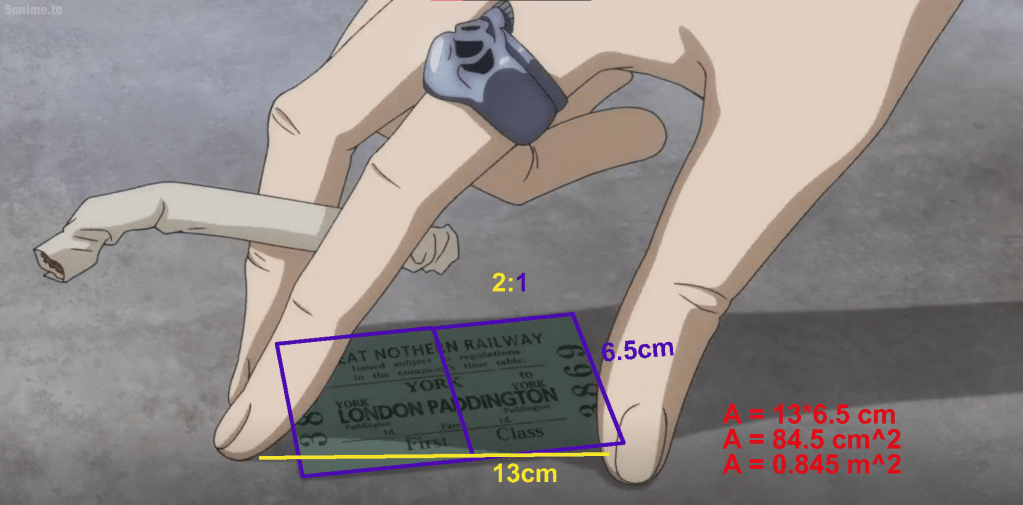
For extra accuracy, I decided here to calculate the actual dimensions of the ticket instead of using standard ticket measurements. We can calculate the width like so: using this picture of Sherlock’s hand, and knowing that the space between the tip of an index finger and a thumb in an outstretched hand (known as the thenar web space, which sounds like a sci-fi location) is 6in (we’ll assume a little over 5in, since the hand is not completely outstretched), we can pin the width down to roughly 13cm. Then, analyzing the aspect ratio of the ticket, we can estimate the height to be 6.5cm (1/2 of width), meaning its dimensions are roughly 6.5x13cm, and its area is about 0.845 m^2, which fits about 7.2 times within the area of the ream (6.16 m^2). Thus, assuming a regular mass distribution, we can calculate the mass of the ticket to be (0.02835kg)/(7.2) = 0.0039375kg. I’m going to leave significant figures out of this for extra silliness.

Now we can get to the first real bit of jank. If the ticket hits Sherlock’s face with 4.4N of force, and the ticket’s mass is 3.9375 * 10^-3, then the ticket’s velocity when it lands is (4.4)/(3.9375 * 10^-3) = ~1117.5 m/s. ONE. THOUSAND. METERS PER SECOND. For context, that is about 13 times the top speed of a bullet train, and 3 times the speed required for a sonic boom. It is several times faster than a B-2 Bomber. And from here, it just keeps getting worse. Watson didn’t just plant the ticket on Sherlock’s face, no, he threw it. That means the ticket, which remained in what is possibly the least aerodynamic shape possible, traveled through about two meters of drag and air resistance before hitting Sherlock.

Now, accurate drag calculations are extremely difficult, and usually require advanced simulations to predict (I’m sure you’ve seen the “aerodynamics of a cow” picture floating around), which is why I don’t whatsoever claim this following section to be accurate– just like the rest of the post, really. That being said, we can try to calculate the drag using this drag formula integrated for distance courtesy of Marcks Thomas in StackExchange. The formula is as follows:

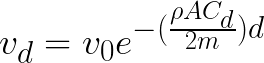
In this equation, v_d represents the final velocity (1117.5 m/s), v₀ the initial velocity, the greek letter of rho the air density (1.225 kg/m^3), A the cross-sectional area (0.845 m^2). C_d the drag coefficient (1.28), m the mass of the ticket (3.9375 * 10^-3 kg), and the distance (I’m going with 2m).

Plugging in all our values, and solving for v₀, we get that the initial velocity is, drumroll please, 1.53948547 * 10^149 m/s. I’m sure that number is completely insignificant to you, so normally I would try to compare it to a regular situation. Except I can’t. Usain Bolt’s fastest sprint was 12.5 m/s. The fastest recorded baseball pitch was 47 m/s. In fact, the speed of light is 3.0 * 10^8 m/s. This ticket wasn’t going at one-fourth the speed of light, it wasn’t going at half the speed of light, it was going at 10^140 times the speed of light. That’s 140 zeroes.

So let’s draw conclusions. First and foremost, that speed is impossible. No object can travel faster than the speed of light, physically speaking. Even if it could, drag couldn’t be used to derive the initial velocity, as an object approaching the speed of light would much rather fuse with the air molecules than push them aside. I could say here that my equations were wrong several times (the card wasn’t traveling straight forward, but at an angle, and it was rotating; it was clearly slower in the video; etc.) However, I could also say that maybe both Sherlock and Watson are beings of extradimensional power, able to withstand forces beyond our wildest imagination. As a friendly reminder, to throw a ticket at a speed of 1.53948547 * 10^149 m/s, Watson would have had to exert a force of 1/2(m)(v)^2 = 1/2(3.9375 * 10^-3 kg)(1.53948547 * 10^149 m/s) = 4.66596804 * 10^295 Joules, or about 10^226 times the mass energy of the observable universe. The Hiroshima bomb we mentioned in the first paragraph? You’d need a decillion decillion decillion decillion decillion decillion decillion decillion decillion decillion decillion decillion decillion of those. 282 zeroes. That ticket, as per Newton’s Third Law, would have exerted an equal force on Watson. But hey, not like we’re really following any laws anymore.

It’s worth noting that Watson is completely fine a few seconds later. Not only that, but the ticket seems to move at a completely reasonable speed, and we see no flash of light that would indicate the end of the universe, so here’s my theory: Watson, enraged at Holmes, let loose a fraction of his incomprehensibly strong power. The cameraman, iconic as always, traveled several trillion times the length of the observable universe to keep up, and Holmes used his equally impossible power to make sure the universe didn’t vaporize instantly. What more, really, can you expect from a Crunchyroll shonen?